Brainy: a simple PHP class for machine learning

Brainy is a PHP class that helps you to create your neural network.
I built Brainy just for fun during my artificial intelligence studies. If you are a web developer and you have just started studying AI, Brainy can be helpful to make the first steps in machine learning; but there is no other good reason to use PHP for machine learning!
I suggest to use Python (or R) instead, because it has thousands of tutorials, documentations and libraries; plus, library like TensorFlow can use the computational power of your GPU!

With brainy you can build a simple neural network that contains just one hidden layer with limitless number of neurons in the input, hidden layer and output layer.

You can download the project from the link below.

In this example I’m going to solve the XOR problem with a neural network with 2 input neurons, 3 neurons in the hidden layer and 1 output neuron. Then we are going to compare the convergence of the learning process using three activation functions.

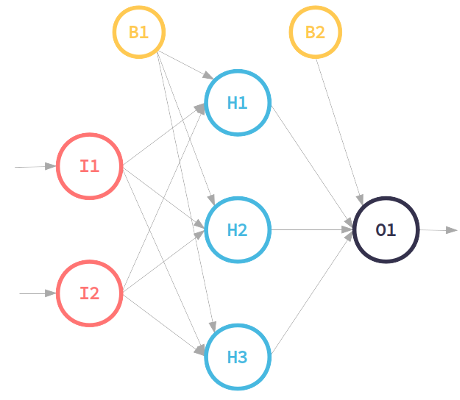
This class implements the class Matrix explained in a previous post.

First step: include the class and instantiate the object:

include 'Brainy.php’;

// choose the learning rate
$learning_rate = 0.001;
// activation functions: relu , tanh , sigmoid
$activation_fun = 'relu’;

$brain = new Brainy($learning_rate , $activation_fun);

• $learning_rate: a constant used in error back propagation learning to affect the speed of learning
• $activation_fun: the activation function to use (Relu, TanH or Sigmoid)

The number of neurons you want in the input and output layers depends on the sizes of the input and output vectors.
The matrix $xor_in contains all the data samples and the matrix $xor_out is the corresponding output of the $xor_in data.

// data samples of XOR input
$xor_in = [ [0,0],
	    [0,1],
	    [1,0],
	    [1,1] ];

// data samples of XOR output
$xor_out = [ [1],
	     [0],
	     [0],
	     [1] ];

So with this configuration we have 2 input neurons (total columns in a row are 2) and 1 output neuron (total columns in a row is 1). Then to have 3 hidden neurons (as you can guess from the picture) the weights matrix between the input layer and the hidden layer must be 3×2 and the weight matrix between the hidden layer and output layer must be 3×1.

For each cycle we are going to propagate forward each input, take the result, compare it with the expected result and then propagate backwards the errors in order to correct the weight matrix and bias matrix.

This is the function to forward the input:
$forward_response = $brain->forward( $input, $w1, $b1, $w2, $b2 );
where:

• $input: is the input vector
• $w1: is the weights matrix between the input and hidden layer
• $w2: is the weights matrix between the hidden layer and output layer
• $b1: is the bias vector of the hidden layer
• $b2: is the bias vector of the output layer

The method forward returns an array of array with the following two keys:

• A: it contains the output vector
• Z: the vector of the outputs of the hidden layer

With the back propagation function we are going to back propagate the errors and try to find the minimum using gradient descend (check the comments in Brainy.php for the formulas).
$new_setts = $brain->backPropagation( $forward_response, $input, $xor_out[$index], $w1, $w2, $b1, $b2 );
where:

• $forward_response: output of the function forward
• $input: input used in forward
• $xor_out[$index]: is the expected output vector (we need it to calculate the errors)
• $w1: is the weights matrix between the input and hidden layer
• $w2: is the weights matrix between the hidden layer and output layer
• $b1: is the bias vector of the hidden layer
• $b2: is the bias vector of the output layer

The method backPropagation returns the new matrices of weighs and bias.

Below is the example where each input is forwarded and back propagated for 10000 times.

$epochs = 10000;
for ($i=0; $i $input) {
		// forward the input and get the output
 		$forward_response = $brain->forward($input, $w1, $b1, $w2, $b2);
	
		// backprotagating the error and finding the new weights and biases
		$new_setts = $brain->backPropagation($forward_response, $input, $xor_out[$index], $w1, $w2, $b1, $b2);
		$w1 = $new_setts['w1’];
		$w2 = $new_setts['w2’];
		$b1 = $new_setts['b1’];
		$b2 = $new_setts['b2’];
	} // end foreach
} // end for $epochs

I did several tests comparing the convergence using different activation functions (Relu, Tanh and Sigmoid): it’s interesting to see how Relu converges quickly to the solution.

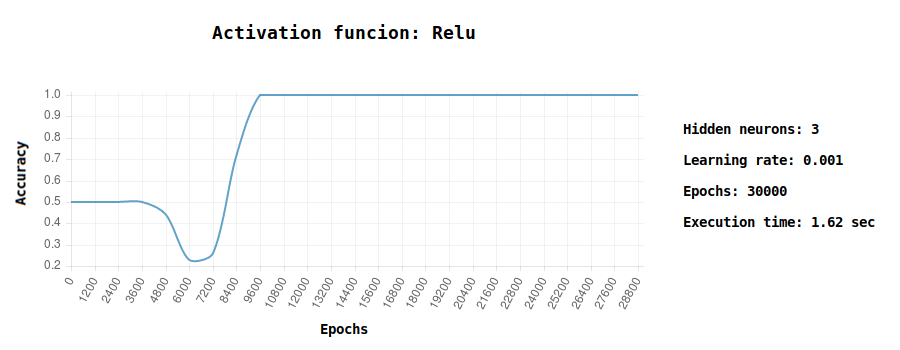
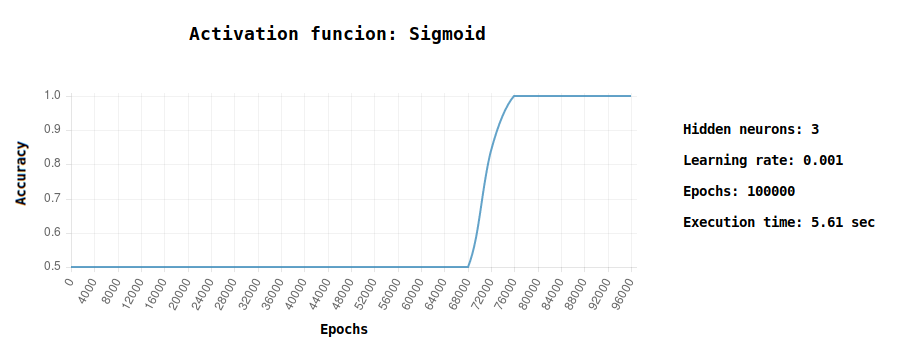
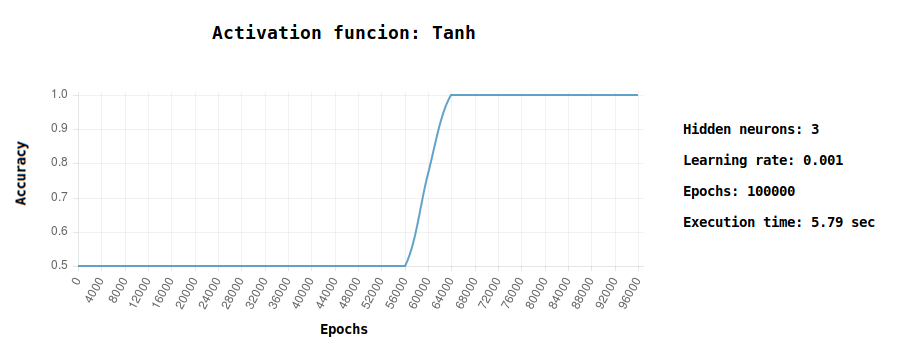
Try yourself to play with different parameters and see how the neural network reacts, for instance:

• Try to increase/decrease the learning rate: you’ll see that with a higher learning rate the neural network can converge quickly but you can miss the minimum and not converge at all.
• Try to add more hidden neurons: you’ll see that the neural network will converge quickly but you are increasing the computational cost.

Have fun _